Daily Maths Challenges

216 readers

1 users here now

Share your cool maths problems.

Complete a challenge:

Post your solution in comments, if it is exactly the same as OP's solution, let us know.
Have fun.

Post a challenge:

Doesn't have to be original, as long as it is not a duplicate.
Challenges not riddles, if the post is longer than 3 paragraphs, reconsider yourself.
Optionally include solution in comments, let it be clear this is not a homework help forums.
Tag [unsolved] if you don't have a solution yet.
Please include images, if your question includes complex symbols, attach a render of the maths.

Feel free to contribute to a series by DMing the OP, or start your own challenge series.

founded 11 months ago

MODERATORS

[email protected]

Infinite product follow-up (links.hackliberty.org)

submitted 10 months ago by [email protected] to c/[email protected]

5 comments fedilink hide all child comments

This is related to the the May 16 post, but takes only the prime indexed terms. Does it still diverge?

Hint

Transform the product into a sum

Hint

The harmonic series 1 + 1/2 + 1/3 + ... 1/n +... diverges

you are viewing a single comment's thread
view the rest of the comments

[–] [email protected] 5 points 9 months ago* (last edited 9 months ago) (1 children)

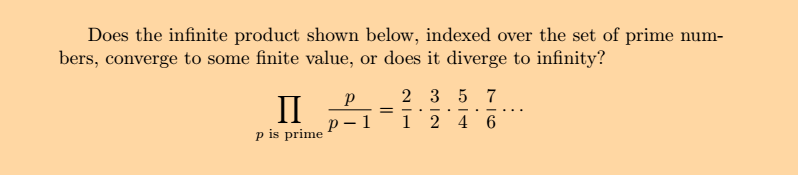
I don't know how to begin proving it, but the more I run this series out, bigger it gets. The conditions of the equation are such that it will always have a consistently non-zero rate of increase, even though that rate of increase decreases each time the formula is cycled ((p~n~/p~n~-1) will always be more than (p~n+1~/p~n+1~-1), nonetheless any and every (p~n~/p~n~-1) will be >1). The divergence will be glacial, but definite.

[–] [email protected] 3 points 9 months ago

I can confirm that your intuition for divergence is correct.