- Estimate 10000!
- Give our answer in form exp{a ln(a) - b ln(b) + c}
- Hint: e
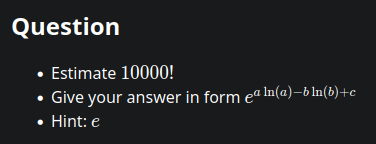
Doesn’t this just follow from Stirling’s approximation?
this post was submitted on 01 May 2024
4 points (100.0% liked)
Daily Maths Challenges
216 readers
1 users here now
Share your cool maths problems.
Complete a challenge:
- Post your solution in comments, if it is exactly the same as OP's solution, let us know.
- Have fun.
Post a challenge:
- Doesn't have to be original, as long as it is not a duplicate.
- Challenges not riddles, if the post is longer than 3 paragraphs, reconsider yourself.
- Optionally include solution in comments, let it be clear this is not a homework help forums.
- Tag [unsolved] if you don't have a solution yet.
- Please include images, if your question includes complex symbols, attach a render of the maths.
Feel free to contribute to a series by DMing the OP, or start your own challenge series.
founded 11 months ago
MODERATORS
Me and my friend from school reinvented the product integral a while back, we tried to approximate x!, later we discovered that what we just did was already done 200 years ago, but to this day I still don't get where the root(2 pi) in Stirling's approximation comes from.
I did a bit of writeup as things happened, slowly finding out that what we're doing isn't original, followed shortly by extreme demotivation.
The sqrt(2 pi) comes from a factor in the derivation of the Stirling formula that is similar to the error integral of the Gauss normal distribution, see Wikipedia (in German, but the formulas should speak for themself ;-) ). The trick Laplace or Poisson came up with, was to replace the integral by its square, ending up with an integral over a 2d domain which is parameterised in polar coordinates to perform the integrations.
The 1st step, squaring the integral, definitely is not really intuitive when doing derivations as a student.